spacetime

A real(istic) time simulator.

spacetime attempts to model time propagation of clocks across the Earth-Moon system. It focuses on how network topology and time synchronization evolve in a growing lunar ecosystem, evaluating both centralized and decentralized Positioning, Navigation, and Timing (PNT) service network configurations.

This book serves as documentation for the spacetime project and a guide to the fundamental concepts that it seeks to model.

Research papers are available in the research-papers section.

If you find a mistake or have a suggestion, please open an issue and let me know about it!

Intuitions for Relativity

This section builds intuitions about relativity and spacetime.

Einstein’s theory of relativity describes how space and time are related based on the logical consequences of two core postulates:

1. The laws of physics are the same in all inertial reference frames.
2. The speed of light is the same in all inertial reference frames and is not affected by the speed of its source.

Demystifying Terms

The term inertial reference frame simply refers to a frame of reference where all objects follow Newton’s first law of motion:

Objects at rest remain at rest, and objects in motion remain in motion at a constant velocity in a straight line, unless acted upon by an external force.

For example, the inside of a car moving along a road at constant velocity and the inside of a stationary house are inertial reference frames.

The special in special relativity refers to the fact that it is a special case of general relativity: situations when objects are moving at constant velocities in a vacuum. When the theory is extended to follow what happens when objects accelerate, it is called general relativity.

From here on out, we will not worry about distinguishing between special or general relativity. They describe the same phenomena.

Here we will ignore the effects of light passing through a medium for the sake of brevity, but know that the physics still holds. This video provides an excellent intuition about how the speed of light can be constant and also how light moves “slower” through a medium.

TLDW; The “true” speed of light is still constant in any medium. The “slower” speed is a sort of illusion caused by “phase kicks” between the light and the medium as electromagnetic waves propagate through the medium.

Having the right mindset

When learning about relativity, it is important to approach the problem from a scientific perspective. The only way to learn about the universe is to make predictions and then test those predictions with measurements.

It is unsatisfying to say “let’s just accept that this is true” but, that’s part of the genius behind Einstein’s work. Einstein asks “What would happen if this is actually true?” Then he follows the logic to see the consequences of that truth and considers what must happen in order for our observations to be consistent with that truth.

Scientists have used this approach to make predictions about the universe for centuries. The predictions are then tested with measurements. If the measurements match the predictions, then we have evidence that suggests the prediction is true. Why is it true? We don’t know. Science cannot answer that question.

Every test science has invented to test relativity is true has shown that the observation matches the predictions made from following Einstein’s theory. We have to accept that we don’t know why because we can’t test which answer might be correct. It is an unanswerable question right now. Maybe someday there will be an invention that lets us know more about the universe but right now this is as far as we get.

More resources

Here are some excellent videos to get started:

• Special Relativity Intuitions
  • Speed of light is constant in all reference frames
  • Everything moves at the speed of light
  • Time dilation and length contraction
• General Relativity Intuitions
  • How gravity bends light even though it has no mass
  • Gravity comes from time curving space
  • Curved spacetime changes trajectories of light and matter

The textbook

OpenStax has multiple textbooks with sections on relativity:

• College Physics 2e
• University Physics Volume 3
• Astronomy 2e

In the coming chapters we’ll see how relativity affects equations of motion for events measured between inertial reference frames. The majority of this work is based on the Relativity chapter in OpenStax University Physics Volume 3. We’ll be using the same notation and examples as the OpenStax book, but I’ll be adding some additional commentary and examples to help solidify the concepts.

Special Relativity

To begin, we develop some intuitions around the consequences of the speed of light being constant and that all velocities are measured relative to some frame of reference (aka, relativity).

To narrow the scope and really dial in our understanding of the fundamentals, consider the special case where all objects are moving at constant velocity, far from any gravity well (aka, special relativity). This is where Einstein started, too.

Let’s follow the logic and see where it takes us.

Einstein’s postulates

Einstein began with two postulates (source):

1. The laws of physics are the same in all inertial reference frames.
2. Light travels in a vacuum with the same speed $c$ in any direction in all inertial frames.

The “laws of physics” in our analysis are then only those that satisfy the first postulate. This also means that there is no “special” inertial reference frame with special properties. There is no “rest frame” or “absolute space”, only motion of one frame relative to another.

The second postulate states that the speed of light has the same definite speed for any observer, regardless of the motion of the source.

So, like Einstein, we will try our best to forget about what we think we know and instead focus on the consequences of the postulates.

Special Relativity

Inertial reference frames

The first key insight is to approach the problem with the understanding that motion is relative to the inertial reference frame of the observer.

In other words, in an inertial reference frame attached to an object that is not accelerating, it is impossible to tell if the object is at rest or moving at a constant velocity.

The speed of light is constant

This statement is more complicated than it seems, but that’s a tale for another time.

• $c$ is defined as the distance traveled by a photon in 1 second.
• $c$ is not a measurement, it is a scientific constant. In fact, the definition of the meter is derived from the distance that light travels in $\frac{1}{299792458}$ seconds.
• Science has accepted that this value, $299792458\text{ m/s}$, is what we have decided to call the speed of light.

It is key to pin the definition of $c$ this way because as we will see later, distance and time are not absolute, they are relative. The time or distance can change depending on the observer’s reference frame, but distance traveled by a photon divided by elapsed time is always $c$.

Special Relativity

Time Dilation

The time experienced by an observer in its inertial frame is called its proper time. Something interesting happens when we compare the proper time of a body at rest to the proper time of a body in motion within the same inertial frame that teaches us an important lesson about the nature of time.

Consider a “light clock” that consists of a photon that bounces between two mirrors set a distance $D$ apart. We count one “tick” of the clock when the photon makes one full round trip. Since the speed of light is constant in all inertial reference frames, an observer will always observe the photon moving at the speed of light, $c$, regardless of the motion of its source.

We see here that both of Einstein’s postulates are satisfied, and we have not violated any laws of physics. Yet two observers measured the photon taking different durations to make the same trip in space. How can this be?

In the astronomer’s reference frame, the photon moves across more space over the course of one “tick” of the clock. The only way the speed of the photon, $c$, can be the same in all reference frames and yet travel across more distance in one reference frame than in another is if the elapsed time experienced by a moving object, $\Delta \tau$, “dilates” compared to the elapsed time experienced by an observer at rest in the reference frame, $\Delta t$.

Therefore, the time dilation equation is:

$$t=\gamma t^{\prime }\text{where}\gamma =1/\sqrt{1-(\frac{v}{c}{)}^2}$$

Special Relativity

Length Contraction

The relative speed between two inertial reference frames, $v$, is the same in both frames. Think about the astronaut and astronomer in the light clock example from the previous chapter.

• The astronaut observes the astronomer moving at a constant speed, $v$.
• The astronomer observes the astronaut moving at a constant speed, $v$.
• The astronomer observes the elapsed time on the astronaut’s clock, $t^{\prime }$, to be dilated by the Lorentz factor, $\gamma$.

Remember the definition of velocity, $v=x/t$. Since we know that the time interval $t$ is dilated by the Lorentz factor, $\gamma$, then the distance traveled by the astronaut, $x^{\prime }$, must also be stretched by $\gamma$ to keep the velocity constant.

$$\begin{gathered} v=x/t,v=x^{\prime }/t^{\prime },t=\gamma t^{\prime } \\ v=\frac{x}{t}=\frac{x^{\prime }}{t^{\prime }},\gamma =t/t^{\prime } \end{gathered}$$ $$x^{\prime }=\frac{x{t}^{\prime }}{t}=\frac{x}{\gamma }$$ $$x^{\prime }=x\sqrt{1-(\frac{v}{c}{)}^2}$$

For any velocity $v$ less than the speed of light, $c$, the length contraction factor is less than 1, meaning the length of the object in the moving frame is shorter than the length of the object in the stationary frame.

General Relativity

Now let’s bring our understanding of relative to the general case where there could be a gravity well nearby (aka general relativity).

General Relativity is a theory of gravity that describes how gravity affects the curvature of spacetime. It builds on the principles of Special Relativity, following the natural consequences of the constancy of the speed of light further and leading to the emergence of gravity and the idea that space and time are not independent axes, but rather our reference frames are composed of a continuous spacetime.

Curved time creates gravity

Reframing our understanding of gravity

In Newtonian physics, gravity is a force that pulls objects together. On Earth, this would look like a uniform force acting on all objects pulling them towards the ground. But our exploration of Einstein’s postulate on inertial reference frames showed us that we can “flip” our reference frame and the physics are the same By this definition it is impossible to tell if you are at rest or in motion. So taking that to the extreme, maybe you are at rest and the Earth is accelerating upwards towards you!

Now consider a photon. It travels in a straight line in space. In the reference frame where Earth is accelerating upwards, after a moment the photon is still traveling in a straight line but the ground is closer to it. More time passes and eventually the ground intersects the photon’s path. From the perspective of the Earth, it looks like the photon is bending towards the ground!

Video: Gravity bends light even though it has no mass

Now let’s get a laser and trace the path of its photons in the Earth’s reference frame. We observe that the photons are bent towards the ground, like before.

This time let’s measure the path of a photon at the top of the beam and at the bottom. To us, it appears that the photon at the top takes a longer path to reach the ground compared to the bottom photon. Our special relativity intuitions remind us that the speed of light is constant, so time must be slower for the top photon compared to the bottom photon. This is called gravitational time dilation.

I find this explanation profoundly unsatisfying. We can do better.

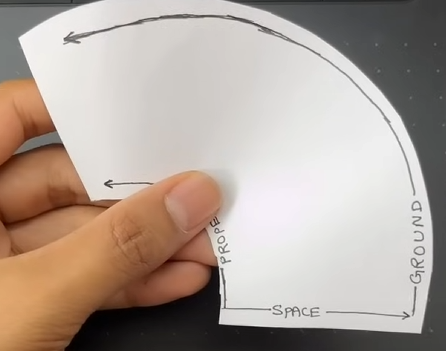
Geometric explanation

A more intuitive way to think about it is to think about it geometrically.

I don’t have the time or skills to make a beautiful animation for this, but the following video does an excellent job of explaining it:

Video: Gravity comes from time curving space

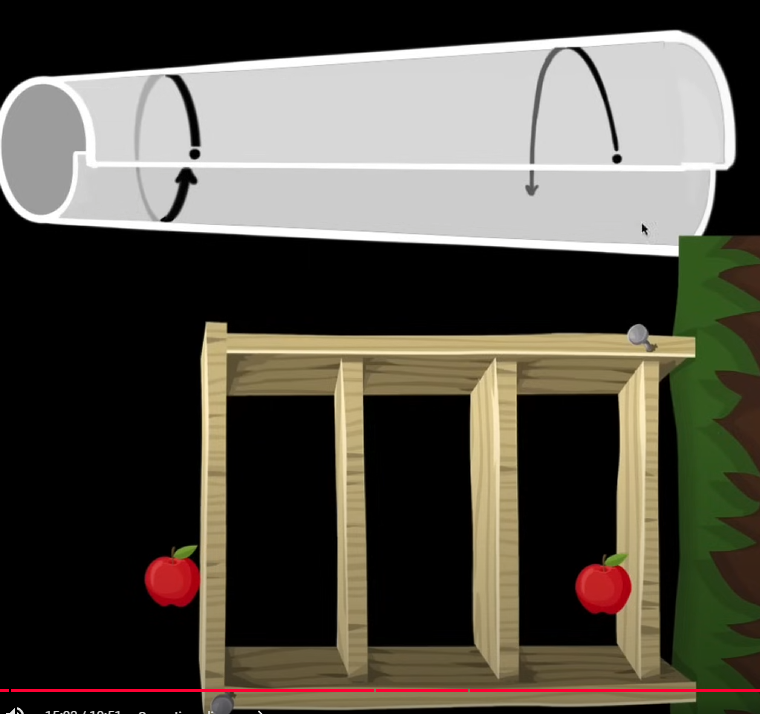
Curved spacetime

A key insight that will help us later is to understand that this definition holds true even if we morph the reference frame. So on the grid, an object would still move from point A to point B with respect to the reference frame. This is what we mean when we say that curved—all objects move along straight lines unless acted upon by a force, but the grid itself is getting morphed by gravity.

Video: Curved spacetime changes trajectories of light and matter

Intuitions for Timekeeping

Network Topology

Lunar Positioning, Navigation, and Timing

Applying Relativity to Vector Math

Now that we’ve come to grips with the fundamental concepts and intuitions of relativity, we can start applying these concepts to vector math.

Special relativity

Coordinate transformations between inertial reference frames

An event, $s$, is a location and time coordinate relative to an inertial reference frame, $S$. For simplicity, we’ll abbreviate the time derivatives as $\dot{s}$ and $\ddot{s}$. I’ve written it out below, expanded out into the $x$, $y$, and $z$ spatial components to remind us that these are vectors in 3D space.

$$\begin{array}{rl}\text{position}& s=\left[\begin{array}{c}x\\ y\\ z\end{array}\right]\\ \text{velocity}& \dot{s}=\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{z}\end{array}\right]=\frac{d\vec{s}}{dt}(t)\\ \text{acceleration}& \ddot{s}=\left[\begin{array}{c}\ddot{x}\\ \ddot{y}\\ \ddot{z}\end{array}\right]=\frac{d^2\vec{s}}{d{t}^2}(t)\end{array}$$

But what if we want to define the same event relative to a moving reference frame, $S^{\prime }$?

Galilean Transformations

Suppose $S^{\prime }$ is moving with respect to $S$ at velocity $\vec{v}$.

In Newtonian mechanics, the transformation between two inertial reference frames is given by the Galilean transformations. This is the same thing you might have done in high school physics or an engineering course.

$$s(t)=s^{\prime }(t)+vt$$

The underlying assumption here is that time $t$ is the same for observers in $S$ and $S^{\prime }$. So the we can simply differentiate the position vector to get the velocity and acceleration vectors for the event in the moving reference frame.

$$\begin{array}{rl}t& =t^{\prime }\\ \text{and}dt& =d{t}^{\prime }\\ \text{therefore}\dot{s}& ={\dot{s}}^{\prime }+v\\ \ddot{s}& ={\ddot{s}}^{\prime }\end{array}$$

Observers in $S$ and $S^{\prime }$ will measure the same acceleration for the event. Because mass is unchanged by the transformation, $F=ma$ the force measured by the observers will be the same and Newton’s laws hold. All is well and you get an $A+$ in physics class.

Testing against Einstein’s postulates

Let’s see if Einstein’s postulate that the speed of light is the same for all inertial reference frames holds when applying the a Galilean transformation.

We can test this by calculating the speed of a photon in $S$ and $S^{\prime }$.

$$\begin{array}{rl}\text{let}\dot{s}=c,{\dot{s}}^{\prime }=c& \\ \text{if}& \dot{s}={\dot{s}}^{\prime }+v\\ \text{then it must be true that}& c=c+v\end{array}$$

This is not true, so the Galilean transformation violates the speed of light postulate!

The issue comes from the assumption that time is the same for observers in $S$ and $S^{\prime }$, which we know from the previous chapter is not true. In most cases, the relative motion $v$ is much smaller than the speed of light, $c$, so the Galilean transformation is a good approximation. But if $v$ is significant compared to $c$ or we want to be very precise over long distances, we need a more accurate transformation that accounts for the effects of relativity.

Lorentz Boosts

Good news, someone already figured this out! The Lorentz transformations are a set of equations that describe how to transform coordinates between two inertial reference frames that are in relative motion and are consistent with the speed of light postulate.

Shorthand for this operation is to call it a Lorentz boost (source).

Vectorized Lorentz Boosts

Wikipedia has a great explanation of how to apply a Lorentz boost to a vector.